Zusammenfassung: Zusammenfassung: Qualitative Forschung lässt sich als eine Forschungskonzeption definieren, bei der der Erhebung und Verarbeitung kategorialer Daten ein großes Gewicht zukommt, die Datenanalyse eher auf deskriptive als auf explikative Ergebnisse abzielt, man der Entwicklung neuer Werkzeuge große Aufmerksamkeit widmet, man lieber klassifiziert als quantifiziert, die valide Operationalisierung von Variablen wichtiger ist, als ihre messtheoretische Absicherung und die Analyse von Effektstärken die Priorität vor der inferenzstatistischen Absicherung von Ergebnissen hat.

Zu der Frage "Wie kommt man von informationsreichen Daten zu brauchbaren Theorien" hat die sozialwissenschaftliche Methodenlehre tatsächlich wenig zu bieten. Wenn die Beseitigung dieses Defizits das Anliegen der Entwicklung "qualitativer Methoden" ist, dann wird auch aus dieser Modeströmung eine wichtige und bleibende Erweiterung unseres Methodenarsenals hervorgehen.

Keywords: Keywords: Metrische Daten, kategoriale Daten, Operationalisierung, Messen, Methoden, Modelle, Quantifizierung, quantitative Forschung, qualitative Forschung

Jeder inhaltlichen Disziplin billigt man Modeströmungen und Anpassungen an den Zeitgeist zu: Was heute ein aktuelles Forschungsthema ist, ist morgen schon Schnee von gestern. [1]

Ganz anders in der Methodenlehre: Die universelle Einsetzbarkeit statistischer Verfahren wie Regressionsanalyse, Faktorenanalyse oder Varianzanalyse, die ehernen Gesetze der Versuchsplanung und der Stichprobentheorie oder die mathematische Exaktheit des conjoint measurement oder des law of comparative judgement überstehen jede Modeströmung schadlos oder scheinen gar gestählt aus ihr hervor zu gehen. Die Werkzeuge einer Disziplin können und dürfen sich nicht so schnell ändern wie die Inhalte der Disziplin, die mit diesen Werkzeugen untersucht werden. [2]

Trotzdem gibt es auch in der Methodenlehre Moden und einen wechselnden Zeitgeist. Sie führen jedoch nicht dazu, dass sich das bisherige Arsenal in Forschungsmethoden als falsch oder unbrauchbar erweist. Vielmehr führen sie dazu, dass sich das Methodenarsenal um wesentliche Teile erweitert und bereichert. [3]

Der Titel "Zeitgeist und Moden empirischer Analysemethoden" soll andeuten, dass sich zwischen zwei Generationen noch andere Dinge abspielen als dass die jüngere Generation von der älteren Generation lernt. Im folgenden möchte ich auf diejenigen Moden eingehen, die ich selbst als maßgeblich für die Methodenentwicklung wahrgenommen und miterlebt habe. [4]

Moden kommen oft als Dichotomien, als Begriffspaare daher, wovon der eine Begriff den klassischen und vermeintlich überkommenen Methodenteil bezeichnet und der andere das bisher sträflich vernachlässigte, das innovative oder vermeintlich revolutionär neue Element der Methodenlehre. Ich möchte im folgenden sieben solcher Dichotomien benennen und jeweils darauf hinweisen, was sie für die Entwicklung der empirischen Forschungsmethodik bedeuten oder bedeutet haben. [5]

Die erste Dichotomie ist diejenige von metrischen Daten und kategorialen Daten. Die Modeströmung, dass sich selbst hart gesottene Statistiker der Analyse kategorialer Daten zuwandten, liegt schon über ein Vierteljahrhundert zurück. Es war damals eine mit viel Emphase vertretene These, dass Menschen – und Menschen sind schließlich das Objekt sozialwissenschaftlicher Forschung – in der Regel keine metrischen Messwerte produzieren, sondern nur kategoriale, bestenfalls ordinale Daten. [6]

Um kategoriale Daten rankte sich damals tatsächlich eine Art Ideologie, die in einem Zitat meines Kollegen und Flurnachbarn, Rolf LANGEHEINE, zum Ausdruck kommt. In seinem Buch mit dem Titel "Loglineare Modelle zur multivariaten Analyse qualitativer Daten", wobei mit qualitativen Daten natürlich kategoriale Daten gemeint waren, zitiert er zwei deutsche Autoren, die im Hinblick auf die Dominanz metrischer Analyseverfahren einen Methodenoktroy diagnostizierten "dessen Wurzeln sie in dem die gegenwärtige Gesellschaft kennzeichnenden System von Warenproduktion und Warentausch sehen" (LANGEHEINE, 1980). [7]

Mögen dies auch noch die letzten Ausläufer der 68-er-Jahre gewesen sein, so ist es doch beeindruckend, welche Vielfalt und Ebenbürtigkeit, wenn nicht gar Überlegenheit sich im Bereich von Methoden für kategoriale Daten gegenüber statistischen Verfahren für metrische Daten entwickelt hat. [8]

Log-lineare Modelle stellen heute ein formales Rahmenmodell dar, das vergleichbar ist mit dem allgemeinen linearen Modell der metrischen Statistik. Strukturgleichungsmodelle mit latenten Variablen, latent state-trait Modelle, Regressionsmodelle, Modelle mit Interaktionen beliebiger Ordnung, stehen für die Analyse kategorialer Daten zur Verfügung (vgl. z.B. ANDRESS, HAGENAARS & KÜHNEL, 1997). [9]

Die log-lineare Methodologie hat die korrelationsstatistische Methodologie sogar als restriktiv entlarvt, basiert diese doch ausschließlich auf den bivariaten Assoziationen einer Menge von Variablen und ist daher in ihrer Mächtigkeit, Wechselwirkungen höherer Ordnung abzubilden, eingeschränkt. [10]

Aber auch die Item-response-Theorie hat ihren rasanten Fortschritt nicht zuletzt der Einsicht oder der Ideologie zu verdanken, dass Tests nicht per se metrische Messwerte liefern, sondern zunächst einmal nur kategoriale Antwortvariablen. Die Liste von statistisch ausgeklügelten Verfahren zur Verarbeitung kategorialer Daten ist um viele Punkte verlängerbar, genannt seien hier nur die logistische Regression, die Konfigurationsfrequenzanalyse (KRAUTH & LIENERT, 1973) und die Feature-pattern-Analysis (FEGER, 1994). [11]

Bei der Beratung von Forschungsprojekten ist man oft mit der Einstellung konfrontiert, dass deskriptive Datenanalysen weniger strenge Anforderungen an die Auswertungsmethoden stellen als explikative, also auf Erklärung abzielende Datenanalysen. Dabei unterliegt es durchaus zeitlichen Schwankungen oder "Modeströmungen", ob man seine Daten "lediglich deskriptiv" auswertet oder sich den strengen Anforderungen explikativer Analysen stellt. Im Wechselspiel dieser Modeströmung hat sich Methodenforschung abgespielt, die der philosophischen Position Vorschub leistet, dass es zwischen Deskription und Explikation eigentlich gar keinen Unterschied gibt. [12]

Arbeiten zum Kausalitätsbegriff in den empirischen Sozialwissenschaften (RUBIN, 1974, STEYER, 1992, STEYER, GABLER, von DAVIER, NACHTIGAL, & BUHL, 2002) lassen den Schluss zu, dass die Absicherung einer Kausalinterpretation nichts anderes darstellt, als eine hinreichend detaillierte Deskription. So ist nach dem sog. starken Kausalitätsbegriff von (STEYER, 1992) die Varianz einer abhängigen Variable B dann und nur dann durch eine unabhängige Variable A erklärbar, wenn die Stärke des Zusammenhangs beider Variablen invariant ist bezüglich aller denkbaren Moderatorvariablen. [13]

Der Nachweis, dass Variable A Variable B beeinflusst und somit "erklärt", besteht im Aufzeigen eines gleich starken Zusammenhangs beider Variablen unter allen denkbaren Bedingungen. Die Erfüllung dieses Kausalitätsbegriffes beinhaltet nichts anderes als eine – zugegebenermaßen sehr detaillierte – Deskription der Daten. [14]

Das Experiment als klassisches Unterscheidungskriterium zwischen deskriptiven und explikativen Analysen dient nach dieser Kausalitätstheorie dazu, alle potenziellen Moderatorvariablen durch Randomisierung zu kontrollieren. Es ist das wesentliche Merkmal eines Experimentes, dass die Versuchspersonen zufällig den Experimentalbedingungen zugewiesen, also randomisiert werden. Aus dieser Perspektive sichert nicht die Manipulation der Treatment-Variable die Kausalinterpretation ab, sondern die Kontrolle aller möglichen Drittvariablen durch die Randomisierung der Versuchspersonen (ROST, 2000a). [15]

Diese Art der Ausschaltung potenzieller Moderatoreffekte durch Randomisierung ist aus Sicht der Kausalitätstheorie jedoch nur das Zweitbeste, was man tun kann. Die Randomisierung als Methode der Kontrolle von Drittvariablen liefert nämlich nur mittlere Effekte, d.h. den Effekt von Variable A auf Variable B, der sich gemittelt über alle Valenzen aller Drittvariablen ergibt. Eine Prüfung der Erfüllung des starken Kausalitätsbegriffes ist damit nicht verbunden, da die Effekte nicht getrennt für verschiedene Werte potenzieller Moderatorvariablen berechnet werden. [16]

STEYER (1993) nennt es die schwache Kausalitätsbedingung, wenn von interpretierten Effekten (wenigstens) gesichert ist, dass es sich um mittlere Effekte handelt. [17]

Aufgrund dieser Überlegungen kommt man zu der fast schon paradoxen Feststellung, dass sich eine Kausalinterpretation von Zusammenhängen und somit eine explikative Datenanalyse durch eine detaillierte Deskription von Daten besser absichern lässt als durch ein Experiment. [18]

Seit Jahrzehnten existieren die Gepflogenheit, Variablen einfach zu operationalisieren, und die Messtheorie nebeneinander, wenn auch ohne allzu intensive gegenseitige Kenntnisnahme. In den Sozialwissenschaften ist es nach wie vor üblich, Variablen durch eine Messvorschrift zu definieren und frei nach dem berühmten Vorbild "Intelligenz ist was der Intelligenztest misst" auch zu sagen "Lebensqualität ist, was mein Lebensqualität-Fragebogen misst" oder "subjektive Werthaltungen sind das, wonach meine fünf Items fragen". [19]

Auf der anderen Seite gibt es ganze Forschungstraditionen von Messtheorien, die zum Ziel haben, Messwerte als solche auszuweisen. Das heißt, bevor man von irgendeiner Operationalisierung oder Messvorschrift sagen kann, sie messe diese oder jene Variable, muss man erst einmal nachweisen, dass sie überhaupt etwas misst. Um diesen Nachweis zu führen, müssen empirische Relationen in den Daten nachweisbar sein, die aus einer Theorie über die zu messende Variable abgeleitet sind. Das brauchen ja nicht gleich die restriktiven Bedingungen einer Guttman-Skala zu sein, es kann ja auch die Bedingung der doppelten Monotonie einer Mokken-Skala sein, oder die bedingte Unabhängigkeit in einem latent-class-Modell. [20]

Ein markantes Beispiel für die Dichotomie "Operationalisieren oder Messen" ist die Unterscheidung von klassischer und probabilistischer Testtheorie, welche nunmehr schon 40 Jahre koexistieren und konkurrieren. Die klassische Testtheorie als Methode, die Summen von Itemantworten als Messwerte zu deklarieren, um danach deren Messwertqualität mit korrelativen Mitteln zu belegen. Und das Rasch-Modell als Methode zur Überprüfung der Frage, ob diese Addition von Itemantworten zu einem Summenscore überhaupt zulässig ist, das heißt zu Messwerten führt. Die eine Theorie überprüft die Annahmen, die die andere ungeprüft anwendet (ROST, 1996, 1999). [21]

Unabhängig davon, ob man Modeströmungen zugunsten der klassischen oder der probabilistischen Testtheorie sieht, die konkurrierende Koexistenz beider Richtungen hat sich als sehr fruchtbar erwiesen. So ist die Klassische Testtheorie in die Allgemeine Theorie der Strukturgleichungsmodelle integriert worden (vgl. STEYER & EID, 1995) und hat vielfältige Differenzierungen erfahren, z.B. in Form von latent state-trait Modellen (s. EID, 1995). Die probabilistische Testtheorie hat sich z.B. in Hinblick auf Item- und Personenfitmaße, bzgl. Modellgeltungstests oder hinsichtlich ihrer Anwendung auf mehrkategorielle Itemantworten zu einer praktikablen Alternative entwickelt (FISCHER & MOLENAAR, 1995, ROST, 1999, 2000b, 2002). [22]

In der modernen Methodenforschung taucht der Begriff "Methoden" praktisch nicht mehr auf. Statt dessen geht es um die Entwicklung von Modellen, um ihre Identifizierbarkeit, um die Anwendung von Modellen, die Geltungskontrolle von Modellen oder ganz unverblümt um die Frage, welches Modell das "most-general-model" ist. Ist es eine Frage des Zeitgeistes oder der Mode, ob man von Modellen oder Methoden spricht? [23]

Der Methodenbegriff betont den Werkzeugcharakter statistischer Analyseverfahren und unterstreicht die Trennung von inhaltlichen Theorien und dem Werkzeug ihrer empirischen Überprüfung. Der Methodenbegriff beansprucht in gewisser Weise Wertneutralität der Verfahren, so wie man einen Hammer zum Nägel einschlagen verwenden kann, aber auch zum Zerstören von Dingen. Der Modellbegriff betont dagegen die Einheit von Forschungsinhalt und Methoden, liegt doch jeder Methode ein Modell des betreffenden Gegenstandsbereiches zugrunde. [24]

Jede Methode beinhaltet die Anwendung eines Modells und die Interpretation der mit einer Methode gewonnen Resultate setzt voraus, dass das der Methode zugrunde liegende Modell auf die Daten passt. Dies gilt bereits für den Korrelationskoeffizienten, dessen Interpretation voraussetzt, dass das Modell einer linearen Beziehung zwischen zwei Variablen den Daten angemessen ist. Der Nachweis, dass es keine nicht-linearen Beziehungen zwischen den beiden Variablen gibt, stellt die Modellgeltungsprüfung dar und der Korrelationskoeffizient ist der Schätzer für den unbekannten linearen Assoziationsparameter einer bivariaten Verteilung. [25]

Spricht man von Methoden, so stellt die Prüfung der Voraussetzungen für die Anwendung dieser Methoden die eigentliche Modellgeltungskontrolle dar (z. B. die Prüfung der Voraussetzungen für eine Varianzanalyse). Die Anwendung der Methode selbst entspricht der Schätzung der Modellparameter und ihrer inferenzstatistischen Absicherung. [26]

Spricht man von Modellen, so befasst man sich hauptsächlich mit der Frage, inwieweit die mit dem jeweiligen Modell verbundene Methode überhaupt auf die Daten anwendbar ist, also mit Fragen der Modellgeltungskontrolle. Die Schätzung der Modellparameter und deren inferenzstatistische Absicherung ist dann eher ein Anhängsel, das bei Modellgeltung trivial ist. Man spricht vom model-based approach, also vom modellbasierten Zugang zu den Daten, wobei das Gegenstück keinen so schönen Namen hat und allenfalls als "werkzeugorientierter" Zugang bezeichnet werden kann. [27]

Gibt es neben dieser unterschiedlichen Perspektive einen substanziellen Unterschied zwischen modellbasierter und werkzeugorientierter Analyse von Daten? Nein, es gibt keinen Unterschied. Es gibt nur einen Unterschied im Selbstverständnis. Der Methodenspezialist suggeriert, er habe für jedes Problem die richtige Methode, das richtige Werkzeug. Das Beherrschen dieses Werkzeugarsenals verleiht dem Methodiker die Macht, die Daten derjenigen auszuwerten, die nicht recht wissen, was sie mit ihren Daten tun sollen. [28]

Ganz anders der Modellspezialist. Er kann mit Daten überhaupt nichts anfangen, wenn ihm nicht gesagt wird, was an den Daten modelliert werden soll. Er ist darauf angewiesen, dass man ihm sagt, welche Variable mit welcher anderen interagieren soll, welche Variable als zeitstabil gilt, welche latenten Variablen es geben soll, ob die Messfehler voneinander unabhängig sind usw. [29]

Mag die Kennzeichnung von Datenanalysen als Anwendung von Methoden oder als Konstruktion von Modellen auch dem Zeitgeist unterliegen, so ist mit dem modellbasierten Zugang eine Vielzahl neuer Modelle und somit neuer Methoden entstanden. Strukturgleichungsmodelle, loglineare-Modelle, Item-response-Modelle sind Begriffe für ganze Klassen und Familien von statistischen Analysemodellen, die auf die jeweiligen Fragestellungen zugeschnittene "Methoden" bereitstellen. Methoden der Datenanalyse werden zunehmend zu Methoden der Modellspezifikation und der Modellgeltungskontrolle. [30]

Dass die Quantifizierung ein Merkmal jeder Wissenschaft ist, der Naturwissenschaften wie der Sozialwissenschaften, scheint common sense zu sein. Das Credo der Messtheoretiker "Whatever exists, it exists in some quantity" ziert so manches Methoden-Lehrbuch, ungeachtet seiner positivistischen Konnotation. Das Gegenstück zur Quantifizierung ist nicht selbst-evident. Vom linguistischen Standpunkt aus betrachtet wäre es vielleicht die "Qualifizierung", aber das ist nicht gemeint. [31]

In der Überschrift dieses Abschnitts ist das Klassifizieren als Gegenstück zum Quantifizieren benannt. Diese Logik lässt sich an den Skalentypen von STEVENS festmachen, bei denen alles oberhalb der Nominalskala, also Ordinal-, Intervall- und Verhältnisskala etwas mit Quantifizieren zu tun hat. Nur die Messung auf Nominalskalenniveau beinhaltet keine Quantifizierung, sondern ist eben Klassifikation. [32]

Sind die quantitativen Skalen in der STEVEN'schen Hierarchie auch die höherwertigen, so sind doch formale Modelle zur Klassifikation allgemeiner als Modelle zur Quantifizierung. Quantifizierung ist ein Spezialfall von Klassifizierung, aber nicht umgekehrt. Dieser Sachverhalt lässt sich intuitiv nachvollziehen, wenn man bedenkt, dass die Klassen, in die eine Menge von Objekten eingeteilt ist, eine bestimmte Struktur haben müssen, um sie als Abstufungen einer quantitativen Dimension interpretieren zu können. Er lässt sich auch formal belegen, z.B. dadurch, dass sich das Rasch-Modell als latent-class-Modell darstellen lässt, aber nicht jedes latent-class-Modell als Rasch-Modell (LINDSAY, CLOGG & GREGO, 1990). [33]

Als (klassifikatorisches) Pendant zum (quantitativen) Credo der Messtheoretiker kann der Titel eines Zeitschriftenartikels von GANGESTAD und SNYDER (1985) herhalten, der da heißt: "To carve nature at it's joints". Die Metapher hebt darauf ab, dass jedes Kontinuum seine Nahtstellen hat, und dass es insbesondere bei den Kontinua, die Messtheoretiker benutzen, sinnvoller sein kann, nach den Nahtstellen zu schauen, an denen ein Qualitätswechsel anstelle eines quantitativen Anstiegs stattfindet. [34]

Auch die Modeströmung des Klassifizierens, wenn es denn eine ist, hat zur Weiterentwicklung der Methoden sozialwissenschaftlicher Forschung geführt. Hier sind neben den schon "klassisch" zu nennenden Clusteranalysen insbesondere die Modelle auf der Grundlage von LAZARSFELDs latent class analysis (LAZARSFELD & HENRY, 1968) zu nennen, aber auch ganz allgemein diskrete Mischverteilungsmodelle (ROST & ERDFELDER, 1996). [35]

Als Gegenstück zur statistischen Signifikanz wird oft die psychologische Signifikanz genannt, womit genau das gemeint ist, was Effektstärkemaße bieten, nämlich eine inhaltliche Beurteilung der Größe eines Effektes oder eines Zusammenhangs. Es gibt immer wieder Modeströmungen, die das eine anstatt des anderen fordern, oder die Frage aufwerfen, was das Wichtigere sei (SEDLMEIER, 1996). Diese Diskussionen sind in gewisser Weise müßig, denn nichts hindert einen daran, in Veröffentlichungen neben der statistischen Signifikanz auch die Effektstärken anzugeben. [36]

Aber auch hier hat die (modebedingte?) Beschäftigung mit dem Thema zu wichtigen neuen Perspektiven geführt. In der Tat hat die Inferenzstatistik heute ernsthaftere Probleme als die Frage, ob sie sich durch Maße der Effektstärke ablösen lassen sollte. Da ist zunächst die "Vertauschung" von statistischer Null- und Alternativ-Hypothese. Während in der klassischen Inferenzstatistik nach NEYMAN und PEARSON in der Nullhypothese für gewöhnlich das Modell spezifiziert ist, das man laut der wissenschaftlichen Theorie nicht erwartet und daher gern verwerfen möchte (z.B. die Gleichheit von Mittelwerten oder ein fehlender linearer Zusammenhang), steht bei "modernen" Modellgeltungskontrollen das interessierende Modell in der Null-Hypothese. Diese Vertauschung hat Implikationen auf die Festlegung und Kontrolle des Alpha- und Beta-Fehlers (ERDFELDER, 1984). [37]

Ein damit zusammenhängendes Problem betrifft den Stichprobenumfang, von dem der Ausgang einer Signifikanzprüfung maßgeblich abhängt. Ein Modell an die Daten anzupassen, d.h. seine Geltung für einen gegebenen Datensatz nachzuweisen, ist bei kleinem Stichprobenumfang sehr leicht möglich, bei sehr großem N dagegen fast unmöglich, da die kleinste Modellabweichung zur Ablehnung des in der statistischen Nullhypothese spezifizierten Modells führt. Das führt zu der paradoxen Situation, dass man z.B. in large scale assessment Studien die Geltung des Messmodells oft nur anhand einer Teilmenge der zur Verfügung stehenden Daten prüft, um das gewünschte Modell beibehalten zu können (ROST, 1999). [38]

Schließlich stellt sich angesichts der Inflation möglicher Modellspezifikationen die Frage, was ein Modellgeltungstest überhaupt noch besagt. Zu jedem Modell, das erfolgreich an die Daten angepasst wurde, lassen sich mehrere Modelle formulieren, die ebenfalls auf die Daten passen. Das gilt für lineare Strukturgleichungsmodelle ebenso wie für log-lineare Modelle oder Item-response Modelle. Eine gelungene inferenzstatistische Absicherung besagt lediglich, dass man ein Modell gefunden hat, das auf die Daten passt. Das Erfreuliche an dieser Entwicklung besteht darin, dass den prä-experimentellen Hypothesen wieder eine größere Bedeutung zukommt. [39]

Bei dieser Dichotomie ist es wohl unstrittig, was derzeit Mode ist: qualitative Forschung ist angesagt, quantitative Forschung ist out. Dabei lässt sich qualitative Forschung als eine Forschungskonzeption definieren, bei der

Diese Charakterisierung nimmt Bezug auf die sechs zuvor genannten Dichotomien und suggeriert damit, dass qualitative Forschung nichts anderes sei, als eine Aneinanderreihung von Modetrends. Auch wenn das viele Kritiker der qualitativen Forschung meinen, soll dies nicht die Botschaft des vorliegenden Beitrags sein. In der Tat tun sich Vertreter der qualitativen Forschung schwer zu definieren, was denn qualitative Forschung ist (s. ROST, 1998). Eine solche Definition kann sicherlich nicht durch Aufzählung erfolgen, sondern muss auf der Ebene der Erkenntnis- und Wissenschaftstheorie anfangen. [41]

Erkenntnisfortschritt durch die empirischen Wissenschaften lässt sich als Wechselspiel von Theorie und Empirie begreifen, wobei man den Weg von theoretischen Konstruktionen zur empirischen Beobachtung als Deduktion, den umgekehrten Weg von der Empirie zur Theorie als Induktion bezeichnet. Wissenschaftlicher Fortschritt lässt sich somit durch ein Kreismodell charakterisieren, in dem sich Deduktionen aus Theorien und Induktionen aus empirischen Beobachtungen abwechseln.

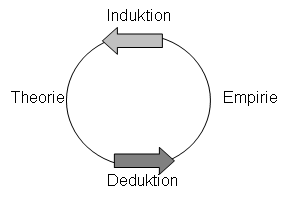
Das Schöne an diesem Kreismodell ist, dass sich der philosophische Streit zwischen Empirismus und Rationalismus, was denn zuerst da gewesen ist, die Theorie oder die Beobachtung, als die unbeantwortbare Frage nach der Henne und dem Ei entlarvt. Um den Erkenntnisfortschritt deutlich werden zu lassen, wird dieses Kreismodell in der Regel zu einem Spiralmodell erweitert (ROST, 2000b). [42]

POPPER (1972) behandelt in seinem Konzept des kritischen Rationalismus ausführlich den Prozess der empirischen Überprüfung einer Theorie, indem aus der Theorie Hypothesen abgeleitet werden und aufgrund empirischer Beobachtung auf den Wahrheitsgehalt der Theorie zurück geschlossen wird. Die Frage, wie man zu seinen Theorien kommt, klammert er ausdrücklich aus dem Gegenstandsbereich der Wissenschaftstheorie aus. Der induktive Schritt von der Empirie zur Theorie besteht nach POPPER nur in der Entscheidung, ob die Beobachtung der Theorie widerspricht oder nicht. Diesem Schritt entspricht in den Sozialwissenschaften die inferenzstatistische Entscheidung über die Beibehaltung der Nullhypothese. [43]

Während man einen großen Aufwand betreibt, aus Theorien prüfbare Hypothesen abzuleiten und diese empirische Prüfung auch durchführt, ist der Schritt von der Empirie zur Theorie vergleichsweise dürftig: Besteht er doch nur in der Absicherung einer binären Entscheidung über den Wahrheitsgehalt der Theorie. Das Kreismodell weist eine von POPPER durchaus gewollte und in den (quantitativen) Sozialwissenschaften praktizierte Asymmetrie hinsichtlich der deduktiven und der induktiven Prozesse auf. [44]

Dieses Ungleichgewicht scheint mir der Gegenstand der (berechtigten) Kritik an "quantitativer Forschung" und somit Ausgangspunkt der "Bewegung" der qualitativen Forschung zu sein. Zu der Frage "Wie kommt man von informationsreichen Daten zu brauchbaren Theorien" hat die sozialwissenschaftliche Methodenlehre tatsächlich wenig zu bieten. Wenn die Beseitigung dieses Defizits das Anliegen der Entwicklung "qualitativer Methoden" ist, dann wird auch aus dieser Modeströmung eine wichtige und bleibende Erweiterung unseres Methodenarsenals hervorgehen. [45]

Andreß, Hans-Jürgen; Hagenaars, Jacques A. & Kühnel, Steffen (1997). Analyse von Tabellen und kategorialen Daten: log-lineare Modelle, latente Klassenanalyse, logistische Regression und GSK-Ansatz. Berlin: Springer-Verlag.

Eid, Michael (1995). Modelle der Messung von Personen in Situationen. Weinheim: Beltz, Psychologie-Verlags Union.

Erdfelder, Edgar (1984). Zur Bedeutung und Kontrolle des ß-Fehlers bei der inferenzstatistischen Prüfung log-linearer Modelle. Zeitschrift für Sozialpsychologie, 15, 18-32.

Fischer, Gerhard H. & Molenaar, Ivo W. (1995). Rasch models – Foundations, recent developments and applications. New York: Springer.

Gangestad, Steve & Snyder, Mark (1985). "To carve nature at its joints": On the existence of discrete classes in Personality. Psychological Review, 92, 3, 317-349.

Krauth, Joachim & Lienert, Gustav A. (1973). Die Konfigurationsfrequenzanalyse (KFA) und ihre Anwendung in Psychologie und Medizin. Freiburg: Alber.

Langeheine, Rolf (1980). Log-lineare Modelle zur multivariaten Analyse qualitativer Daten. München: R. Oldenbourg Verlag.

Lazarsfeld, Paul F. & Henry, Neil W. (1968). Latent structure analysis. Boston: Houghton Mifflin Co.

Lindsay, Bruce G.; Clogg, Clifford C. & Grego, John M. (1991). Semiparametric estimation in the Rasch model and related exponential response models, including a simple latent class model for item analysis. Journal of the America Statistical Association, 86, 96-107.

Rost, Jürgen (1998). Drei Thesen zum Konzept qualitativer Forschungsmethoden. Zeitschrift für Didaktik der Naturwissenschaften, 4, 35-42.

Rost, Jürgen (1999). Was ist aus dem Rasch-Modell geworden? Psychologische Rundschau, 50, 140-156.

Rost, Jürgen (2000a). Allgemeine Standards der Evaluationsforschung. In Willi Hager, Jean-Luc Patry & Hermann Brezing (Hrsg.), Handbuch Evaluation psychologischer Interventionsmaßnahmen Standards und Kriterien (S.129-140). Bern: Huber.

Rost, Jürgen (2000b). The growing family of Rasch models. In Anne Boomsma, Marijtje van Duijn & Tom A.B. Snijders (Hrsg.), Essays on item response theory (S.2-42). New York: Springer.

Rost, Jürgen (2002a). When personality questionnaires fail to be unidimensional. Psychologische Beiträge, 44, 108-125.

Rost, Jürgen (2002b). Qualitative und Quantitative Methoden in der fachdidaktischen Forschung. In Kay Spreckelsen, Kornelia Möller & Andreas Hartinger (Hrsg.), Ansätze und Methoden empirischer Forschung zum Sachunterricht (S.71-90). Bad Heilbrunn/Obb.: Klinkhardt.

Rost, Jürgen & Erdfelder, Edgar (1996). Mischverteilungsmodelle. In Edgar Erdfelder, Rainer Mausfeld, Thorsten Meiser & Georg Rudinger (Hrsg.), Handbuch quantitative Methoden (S.333-348). Weinheim: PVU.

Rubin, Donald B. (1974). Estimating causal effects of treatments in randomized and nonrandomized studies. Journal of Educational Psychology, 63, 688-701.

Sedlmeier, Peter (1996). Jenseits des Signifikanztest-Rituals: Ergänzungen und Alternativen. Methods of Psychological Research Online (MPR-online), 1(4), 45-68. Verfügbar über: http://www.mpr-online.de/.

Steyer, Rolf (1992). Theorie kausaler Regressionsmodelle (Theory of causal regression models). Stuttgart: Gustav Fischer.

Steyer, Rolf; Gabler, Siegfried; von Davier, Alina A.; Nachtigall, Christof & Buhl, Thomas (2000). Causal Regression Models I: Individual and Average Causal Effects. Methods of Psychological Research Online (MPR-oneline), 5(2), 39-70. Verfügbar über: http://www.mpr-online.de/.

Prof. Dr. Jürgen ROST, Wissenschaftlicher Direktor und stellvertretender Leiter der Abteilung Biologiedidaktik am IPN, apl. Professor für Psychologie an der CAU Kiel.

Leibniz-Institut für die Pädagogik der Naturwissenschaften IPN
Institute for Science Education
Olshausenstr. 62
D - 24098 Kiel

Rost, Jürgen (2003). Zeitgeist und Moden empirischer Analysemethoden [45 Absätze]. Forum Qualitative Sozialforschung / Forum: Qualitative Social Research, 4(2), Art. 5, http://nbn-resolving.de/urn:nbn:de:0114-fqs030258.

Forum Qualitative Sozialforschung / Forum: Qualitative Social Research (FQS)

ISSN 1438-5627

Creative Commons Attribution 4.0 International License